Proofs

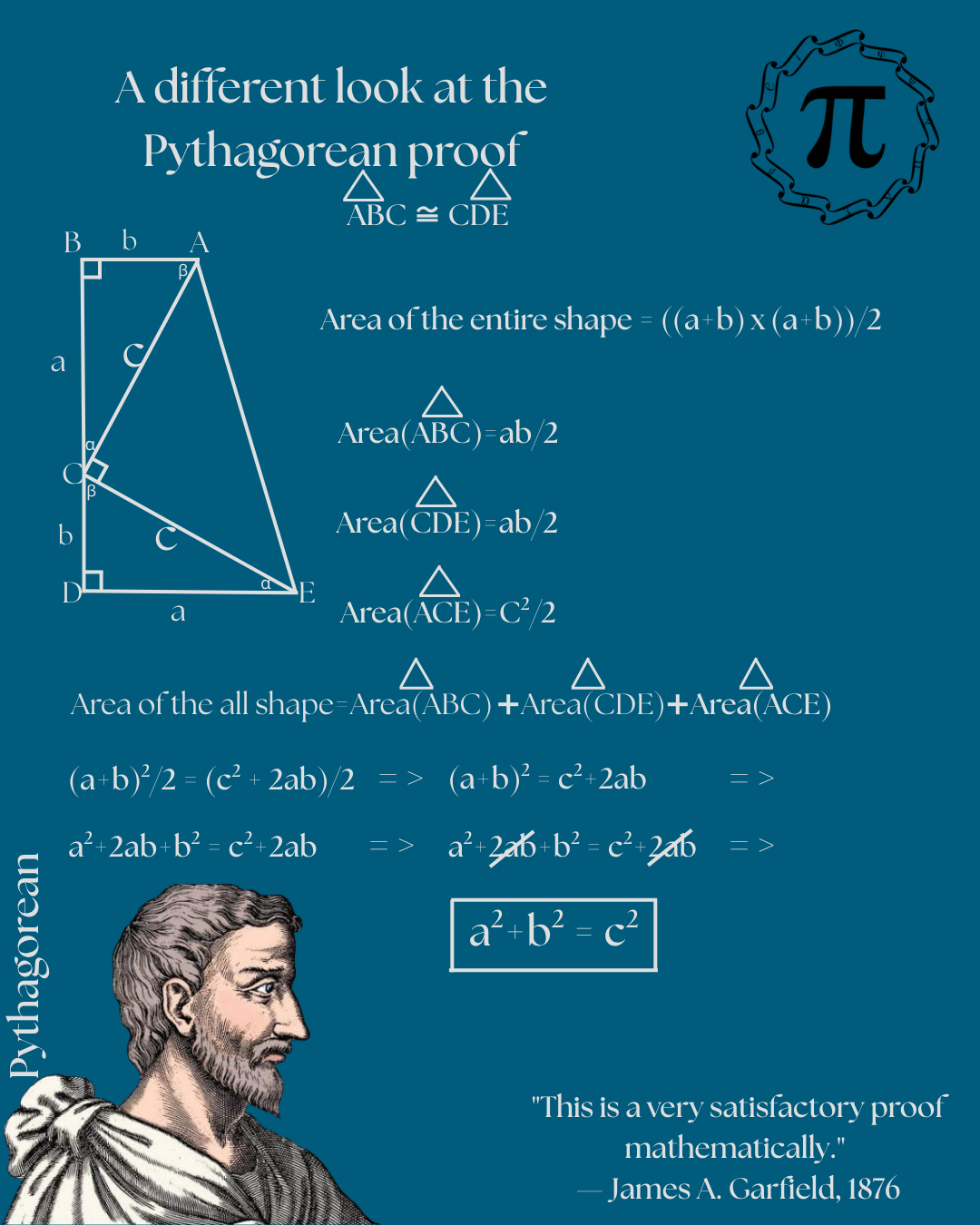
📐 In a right triangle, the square of the hypotenuse equals the sum of the squares of the other two sides:
a² + b² = c²

One of the proofs of this simple yet powerful relation was given in 1876 by then U.S. President James A. Garfield. However, the history of the Pythagorean Theorem goes much further back. 📜

Ancient Egypt, Mesopotamia, China, and India civilizations discovered this relationship before Pythagoras and used it in many fields such as architecture, land surveying, astronomy, and everyday calculations. For example, Babylonian tablets contain numerical examples of this relation, while in China and India, the theorem was approached through geometric and algebraic methods.

With a history going back thousands of years, this theorem remains one of the fundamental pillars of modern mathematics.

Quadratic equations, one of the fundamental building blocks in mathematics, appear in many fields from everyday life to engineering. The formula we use to solve these equations actually dates back to the 9th century.

🔍 Historical Journey: Al-Khwarizmi The foundations of this formula trace back to the great scholar Al-Khwarizmi, regarded as the founder of algebra. His book “Al-Kitab al-Mukhtasar fi Hisab al-Jabr wal-Muqabala” not only influenced mathematics but also introduced the term "algebra" to Western languages.

Thanks to this formula, we can easily find the real roots of any quadratic equation. 🔺 The discriminant value (delta) also tells us how many roots the equation has and whether these roots are real.

📜 In short, this is not just a formula but a centuries-old mathematical heritage.

📐 Golden Ratio (ϕ) The universal language of mathematical aesthetics, the golden ratio, is approximately equal to 1.618. It is defined as the ratio of the larger part to the smaller part when a length is divided into two parts at a point, and if this ratio is 1.618, it is said to have the golden ratio. For example, a rectangle with one side 1.618 units and the other side 1 unit possesses the golden ratio.

🔍 Historical Roots The concept of the golden ratio has been used as a foundation of aesthetic order across many cultures and eras—from the pyramids of Ancient Egypt to Ancient Greek temples, from Renaissance art to Islamic architecture.

The golden ratio appears everywhere, from the symmetry of nature to unique works of art. 📜 The aesthetics of mathematics: The Golden Ratio.

🔷 Cosine Theorem

The Cosine Theorem establishes the relationship between sides and angles in any triangle. It is especially used to find unknown sides or angles in non-right triangles.

📐 Basic formula:

c² = a² + b² − 2ab · cos(α)

This formula is one of the most important bridges connecting trigonometry with geometry.

🧠 Proof Method

A height is drawn from one vertex to the opposite side. Side lengths are expressed using sine and cosine. Then, using the Pythagorean theorem and the identity cos²(α) + sin²(α) = 1, the formula is derived.

📐 Sine Theorem

There is a very special balance between the lengths of the sides of a triangle and the sines of their opposite angles. This relationship is expressed as: a / sin(α) = b / sin(β) = c / sin(γ) = 2R Here, R is the radius of the circumscribed circle around the triangle. Thanks to this ratio, we can practically calculate a missing side or angle.

🔍 How is the proof done?

The proof of the theorem is actually quite elegant. It is done using the relationship of angles with the circumcircle and the definition of sine. By drawing the height inside the triangle and using the central angle–inscribed angle relationship, this ratio emerges. A simple but effective method!

📚 Where does this knowledge come from?

The sine theorem is the result of trigonometric knowledge developed over centuries across different regions. Its foundations were laid in Ancient Greece, systematized by scholars like Al-Biruni and Nasir al-Din al-Tusi in the Islamic world, and this heritage was passed to Medieval Europe, becoming one of the cornerstones of modern trigonometry.

📐 Sine Area Theorem

To find the area of a triangle, you don’t necessarily need to draw the height. If we know two sides and the angle between them, here is the formula: Area = (1/2) · a · b · sin(γ) This method offers a nice trigonometric alternative to the classic "base × height" approach. It is especially a quick and effective solution in problems where sides and angles are given.

🔍 How Does This Work?

The idea behind the theorem is quite simple yet clever: The height formed by the angle between two sides is indirectly expressed using the sine function. In other words, sin(γ) represents the hidden height. This makes area calculation much more flexible and general.

📚 Where Is It Used?

This formula appears not only in math classes but also in many fields such as astronomy, cartography, physics, and computer graphics. Whether you draw a star triangle in the sky or a shape on a computer screen—if there are two sides and an angle, you can easily find the area using this formula.

🔺 What is Menelaus Theorem? Menelaus Theorem is a ratio relation established on triangles in the field of geometry. If a line cutting the sides of a triangle satisfies certain conditions, this theorem allows us to calculate the ratio of the lengths between these points. Especially when a line is drawn that is not parallel to one side of the triangle, it helps us understand how this line divides the triangle’s sides in certain ratios. This theorem is named after the ancient Greek mathematician and astronomer Menelaus. Menelaus first used this ratio relation in astronomical calculations. In ancient times, these ratio relations were useful in many applications such as determining the positions of stars, map drawing, and constructing large structures. Today, Menelaus Theorem is an important tool for solving complex problems involving triangles and is often used as an intermediate step in proofs.

🔺 What is Ceva's Theorem? Ceva's Theorem is a geometric rule that helps us determine whether certain line segments drawn inside a triangle intersect at a single point. Imagine drawing a line from each vertex of a triangle to the opposite side. For these lines to intersect at one common point, a specific ratio relation must hold true. This relation is given by Ceva's Theorem. The theorem is named after the 17th-century Italian mathematician Giovanni Ceva. Ceva developed this rule to understand how special points inside a triangle arise. Historically, Ceva's Theorem was used to find points of balance and structural centers. It has been useful in many fields ranging from cartography to engineering. Today, it still plays an important role in geometry problems for locating hidden points within triangles. If we want to understand what happens inside a triangle, Ceva's Theorem is one of the most powerful guiding tools.

📘 Divisibility Rules for 7, 11, and 13

"Not just memorization, but a product of a mathematical system!" Have you ever wondered about divisibility rules? Especially for prime numbers like 7, 11, and 13, these rules were discovered thanks to modular arithmetic. Each digit has a different "weight." But how exactly?

🔢 Divisibility by 7

Multiply each digit of the number from right to left by the following pattern: +1, +3, +2, -1, -3, -2, ... 📌 Then sum these results. 👉 If the total is divisible by 7, the number itself is divisible by 7.

🔢 Divisibility by 11

Sum the digits from right to left, alternately adding and subtracting: a₀ - a₁ + a₂ - a₃ + ... 📌 If this sum is divisible by 11, then the number is divisible by 11.

🔢 Divisibility by 13

This one is a bit more complex but follows the same idea. 📌 Multiply the digits by the powers of 10 modulo 13: 1, -3, -4, -1, 3, 4, ... 👉 If the total is divisible by 13, then the number is divisible by 13.

📜 Why did mathematicians develop these rules?

Divisibility rules were developed as shortcuts for quick calculations. In the past, instead of dividing large numbers with paper and pencil, these rules were used. Even today, this way of thinking continues to have an impact in fields like cryptography and computer science.

📘 Divisibility Rules for 19 and 37

"Small tips for big numbers!" Divisibility rules for large prime numbers like 19 and 37 might sound mysterious, but they are again based on modular arithmetic! The weights of digits follow a special pattern according to these numbers.

🔍 So how were these rules discovered?

These rules are formed by calculating the powers of 10 modulo 19 and modulo 37. In this way, each digit gains a "weight" based on how the number behaves in that modulo.

📜 Why are they important?

It used to be difficult to divide large numbers mentally. Mathematicians managed to quickly test divisibility using these rules. Even today, they remain important tools for understanding mathematical thinking and algorithms.

💡 What is Fermat’s Little Theorem?

For a prime number p and a natural number a that is coprime to p:
👉 ap ≡ a (mod p)

This theorem is a powerful tool in modular arithmetic. It deals with the remainders of numbers when divided by primes.

📜 Fermat developed this theorem in the 1600s, and it was used for many years in primality testing and fields like cryptography. It is especially one of the foundations of the RSA algorithm!

🔍 What is Mathematical Induction?

Induction is a method of proof where a statement is first shown to be true for a starting value, and then shown to hold for the next value assuming it's true for the current one—thereby proving it for all natural numbers.

It works like a "domino effect" in mathematics:
🎯 If the first domino falls, and
🎯 Each domino knocks over the next,
➡️ Then all dominos will fall!

📐 Trigonometric Ceva Theorem: The Powerful Union of Geometry and Trigonometry!

In a triangle, if three lines intersect at a single point, it’s not just an aesthetic coincidence — it’s a sign of a deep mathematical order.

🔍 To explain this order, the original Ceva’s Theorem was proposed in the 17th century by the Italian mathematician Vincento Ceva.
Later, a version involving the sines of angles instead of side ratios was developed, known as the Trigonometric Ceva’s Theorem.

📚 Where does it show up?

• The incenter of a triangle (center of the incircle)
• The centroid and medians
• Analyses involving cevians (line segments from a vertex to the opposite side)
• Triangle solving problems and math olympiad questions

🧠 The Depth of Trigonometric Ceva

Did you know there’s such a profound relationship behind lines connecting the corners of a triangle?
Now you do! Trigonometry gives geometry a breath of fresh air. 😌