Pisagor Teoremi
.png)
📐 Dik üçgende hipotenüsün karesi, diğer iki kenarın kareleri toplamına eşittir:
a² + b² = c²
Bu sade ve güçlü bağıntının ispatlarından biri, 1876 yılında dönemin ABD Başkanı James A. Garfield tarafından yapılmıştır. Ancak Pisagor Teoremi’nin geçmişi çok daha eskiye dayanır. 📜
Eski Mısır, Mezopotamya, Çin ve Hint uygarlıkları bu ilişkiyi Pisagor’dan önce keşfetmiş ve mimariden arazi ölçümüne, astronomiden günlük hesaplamalara kadar pek çok alanda kullanmıştır. Örneğin Babil tabletlerinde bu bağıntıya dair sayısal örnekler yer alırken, Çin ve Hindistan’da teorem geometrik ve cebirsel yaklaşımlarla ele alınmıştır.
Geçmişi binlerce yıl öncesine dayanan bu teorem, hâlâ modern matematiğin temel taşlarından biridir.





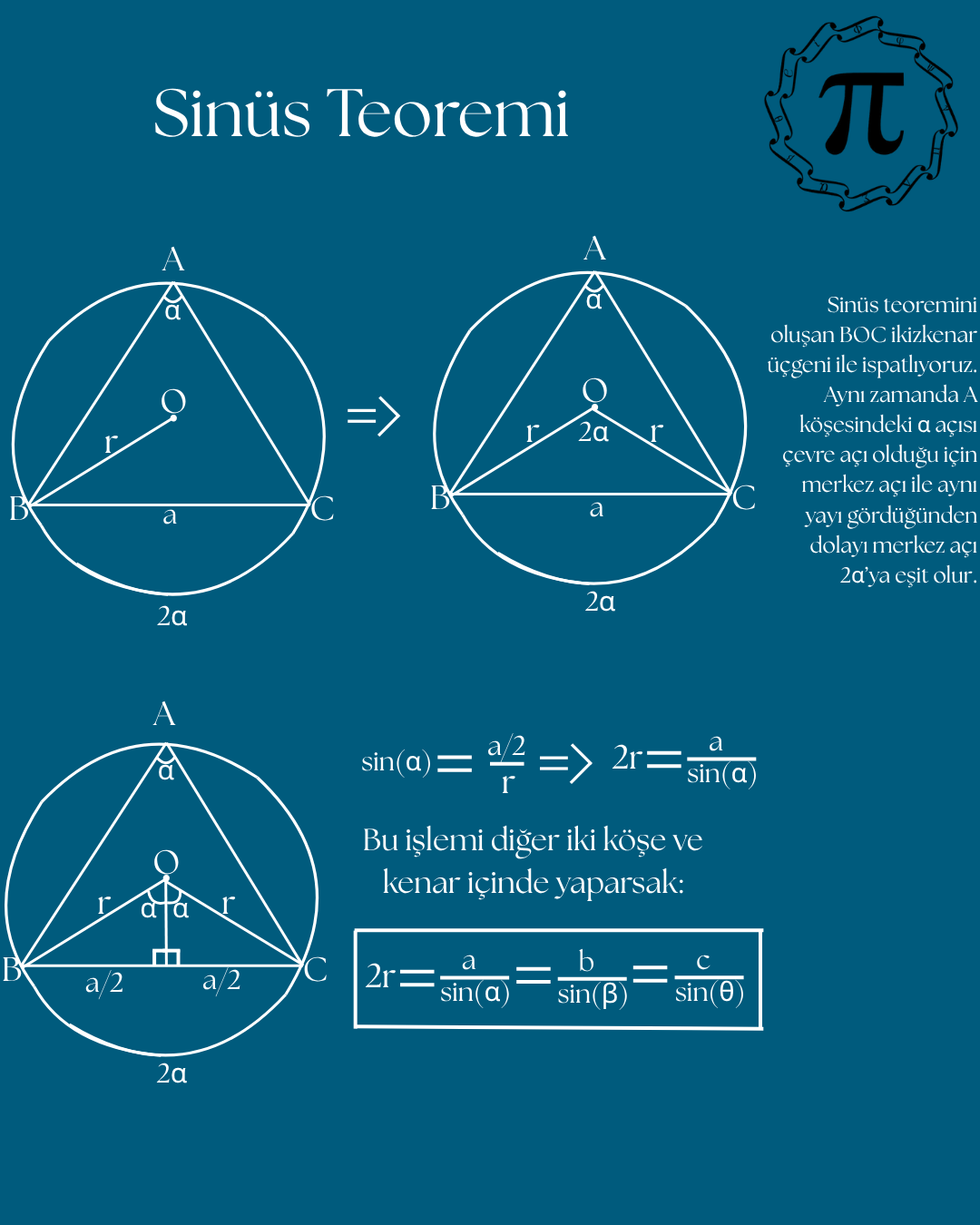
.png)
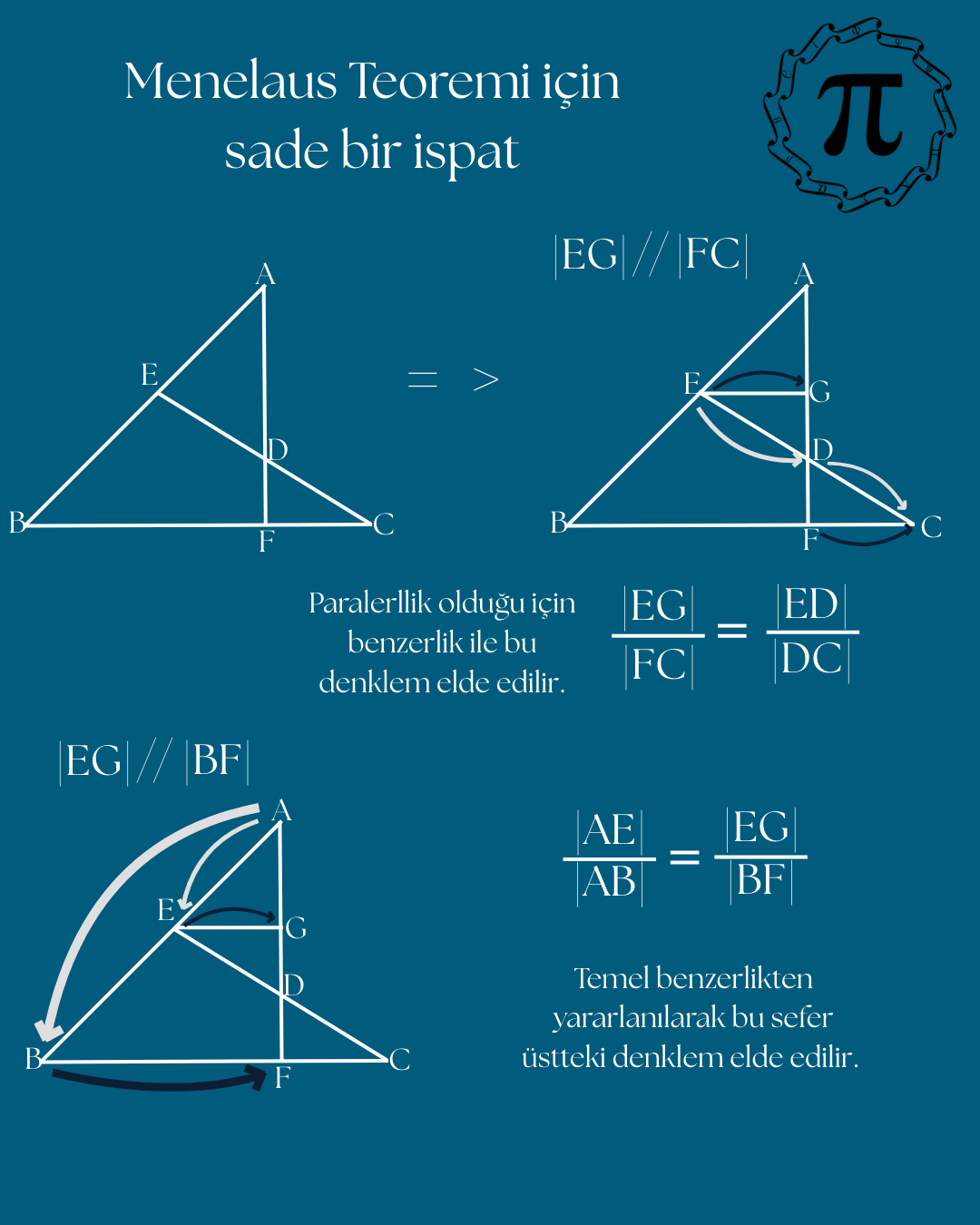
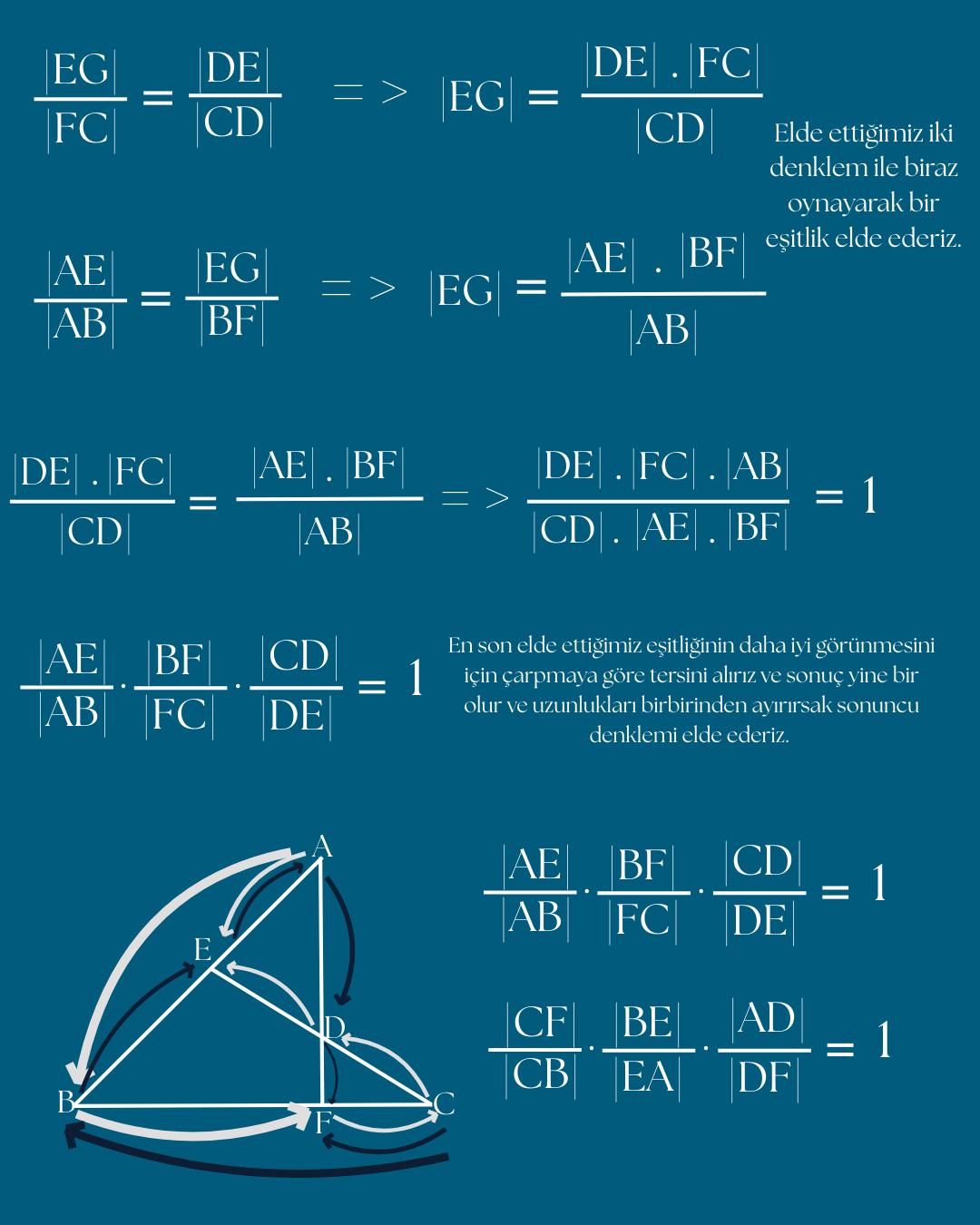
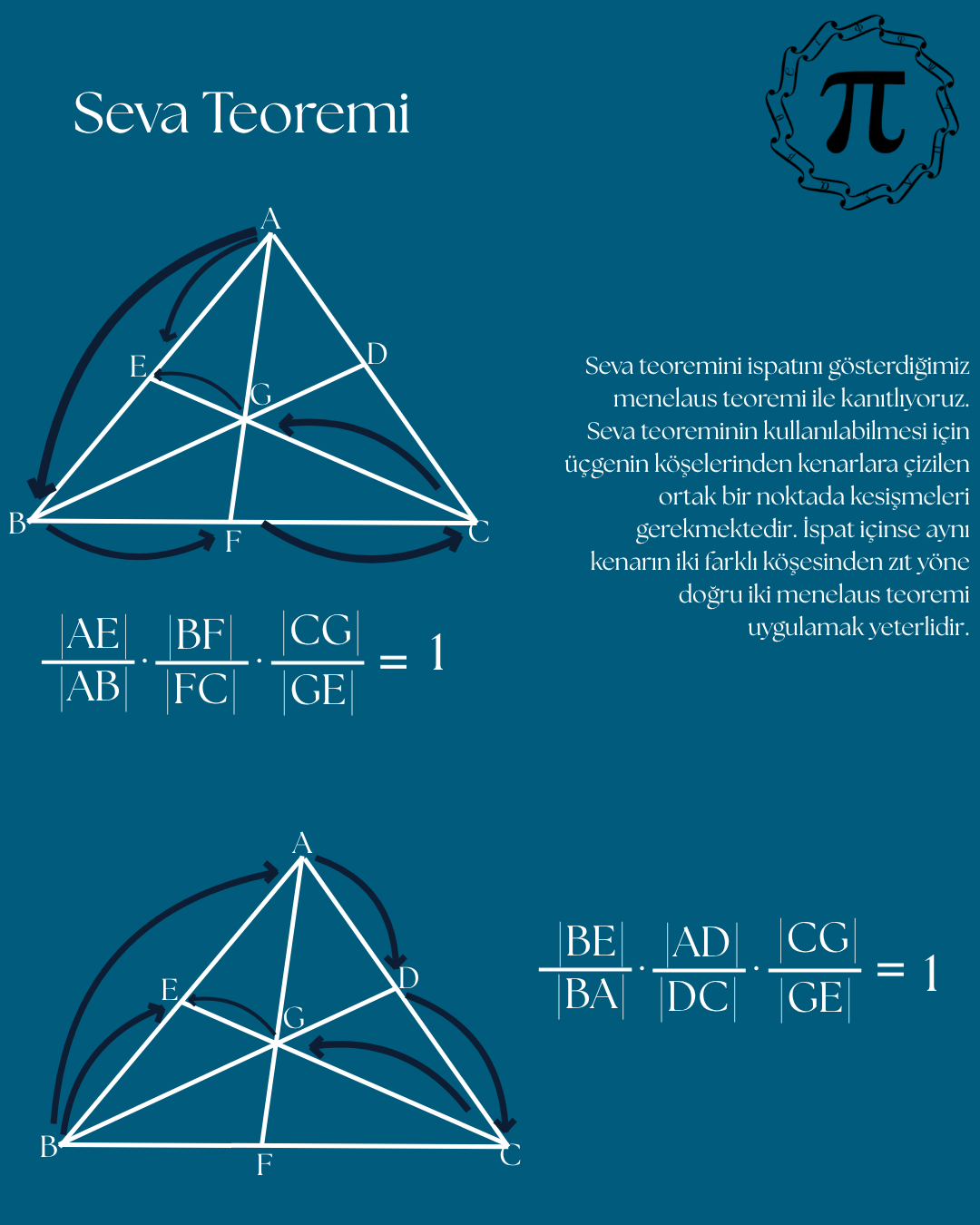
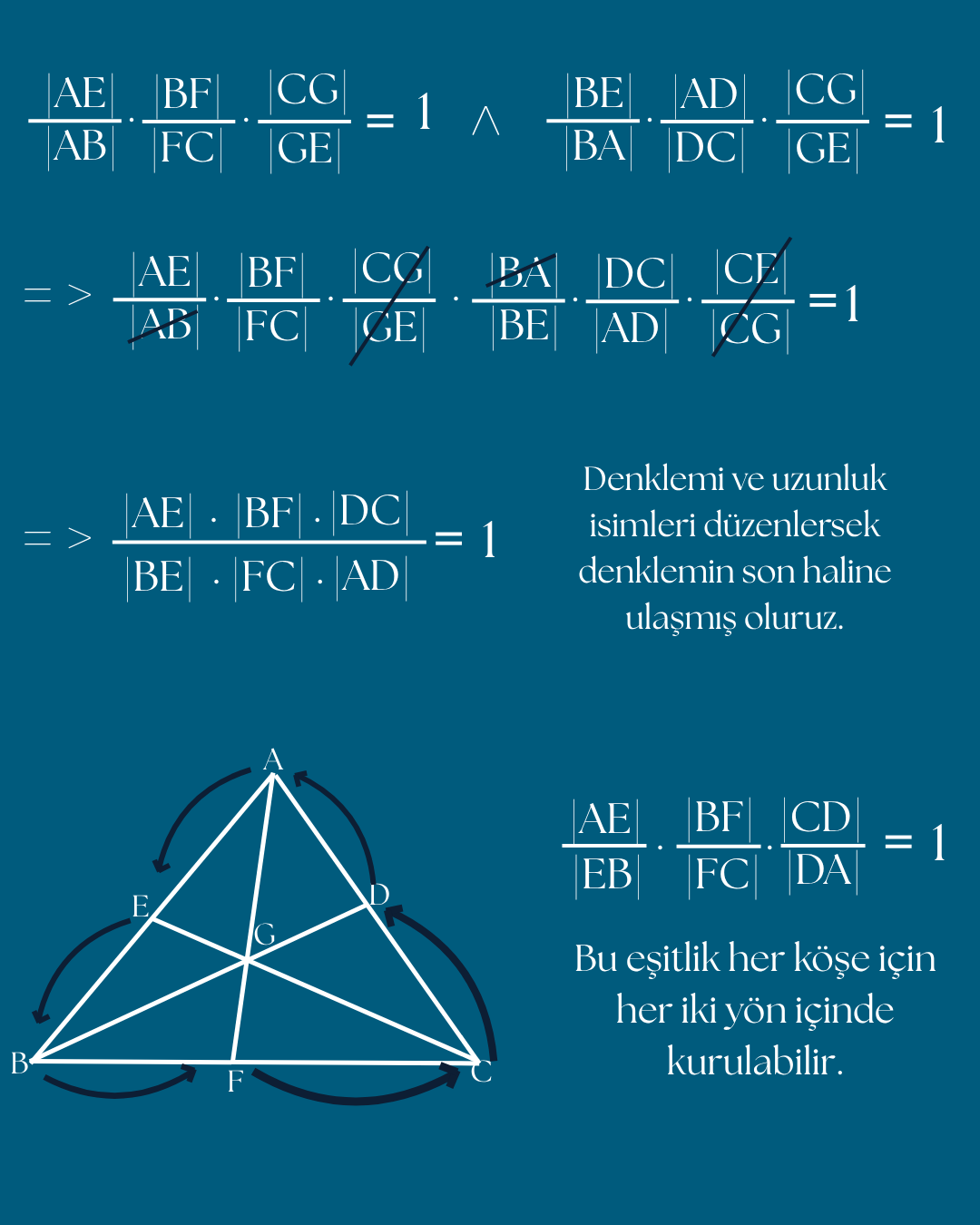
/13.png)
/14.png)
/15.png)
/16.png)
/17.png)










